初三数学中考模拟试题_初三数学中考模拟试题及答案

初三数学中考模拟试题_初三数学中考模拟试题及答案

       下面，我将用我自己的方式来解释初三数学中考模拟试题的问题，希望我的回答能够对大家有所帮助。让我们开始讨论一下初三数学中考模拟试题的话题。

1.������ѧ�п�ģ������

2.2011数学中考模拟试题？

3.中考数学试题参考(附解析)

4.重庆一中初2011级初三(下)6月中考数学模拟试题的第25题（今明两天内）

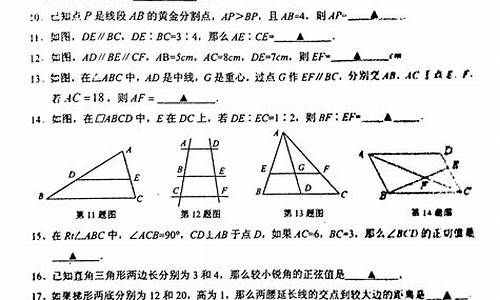
������ѧ�п�ģ������

       此题最简单的方法是用勾股定理加方程。

       解：∵ABCD为矩形

       ∴∠A=∠D=∠ABC=∠DCB

       ∴△APB,△PDC为直角三角形

       ∵△PHF为直角三角形

       ∴△APB,△PDC,△PHF都是直角三角形

       设AP为X，则PD=10-X

       ∴BP?=X?+4?，PC?=（10-X）?+4?

       BC?=10?=100

       ∵△PBC为直角三角形

       ∴X?+4?+（10-X）?+4?=100

       ∴X?-10X+16=0

       ∴X?-10X+25-25+16=0

       ∴（X-5）?=9

       ∴X-5=±3

       ∴X=8或2

       答：能，AP长为8或2

2011数学中考模拟试题？

       一、单点运动

       例1.（2006长春）如图，在平面直角坐标系中，两个函数y=x， 的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动，作PQ//x轴交直线BC于点Q，以PQ为一边向下作正方形PQMN，设它与ΔOAB重叠部分的面积为S。

       （1）求点A的坐标。

       （2）试求出点P在线段OA上运动时，S与运动时间t（秒）的关系式。

       （3）在（2）的条件下，S是否有最大值？若有，求出t为何值时，S有最大值，并求出最大值；若没有，请说明理由。

       （4）若点P经过点A后继续按原方向、原速度运动，当正方形PQMN和ΔOAB重叠部分面积最大时，运动时间t满足的条件是__________。

       解：（1）由 ，可得

       ∴A（4，4）。

       （2）点P在y=x上，OP=t，

       则点P坐标为（ ）。

       点Q的纵坐标为 ，并且点Q在 上。

       ∴ 。

       点Q的坐标为（ ）

       PQ 。

       当

       当 时，

       当点P到达A点时，

       当 时，

       （3）有最大值，最大值应在 中，

       当 时，S的最大值为12。

       （4）

       二、双点运动

       例2.（2006广安）如图所示，在平面直角坐标系xOy中，正方形OABC的边长为2cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线 经过点A、B，且 。

       （1）求抛物线的解析式。

       （2）如果点P由点A开始沿AB边以2cm/s的速度向点B移动，同时点Q由点B开始沿BC边以1cm/s的速度向点C移动。

       ①移动开始后第t秒时，设 ，试写出S与t之间的函数关系式，并写出t的取值范围；

       ②当S取得最小值时，在抛物线上是否存在点R，使得以P、B、Q、R为顶点的四边形是平行四边形？如果存在，求出R点的坐标，如果不存在，请说明理由。

       解：（1）据题意知：

       A（0，－2），B（2，－2）

       ∵A点在抛物线上，∴

       由AB=2知抛物线的对称轴为：x=1

       即：

       ∴抛物线的解析式为：

       （2）①由图象知：

       即

       ②假设存在点R，可构成以P、B、R、Q为顶点的平行四边形。

       ∵

       ∴

       ∴ 。这时 ，BQ=0.8，P（1.6，－2），Q（2，－1.2）

       分情况讨论：

       A）假设R在BQ的右边，这时 ，则：

       R的横坐标为2.4，R的纵坐标为－1.2，

       即（2.4，－1.2）

       代入 ，左右两边相等

       ∴这时存在R（2.4，－1.2）满足题意。

       B）假设R在BQ的左边，这时 ，则：

       R的横坐标为1.6，纵坐标为－1.2，

       即（1.6，－1.2）

       代入 ，左右两边不相等，R不在抛物线上。

       C）假设R在PB的下方，这时 ，则：

       R（1.6，－2.4）代入 ，左右不相等，R不在抛物线上。

       综上所述，存在一点R（2.4，－1.2）

       三、直线运动

       例3.（2006锦州）如图，在平面直角坐标系中，四边形OABC为菱形，点C的坐标为（4，0），∠AOC=60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线l与菱形OABC的两边分别交于点M、N（点M在点N的上方）。

       （1）求A、B两点的坐标；

       （2）设ΔOMN的面积为S，直线l运动时间为t秒（ ），试求S与t的函数表达式；

       （3）在题（2）的条件下，t为何值时，S的面积最大？最大面积是多少？

       解：（1）∵四边形OBABC为菱形，点C的坐标为（4，0）

       ∴OA=AB=BC=CO=4。

       过点A作AD⊥OC于D。

       ∵∠AOC=60°，

       ∴OD=2， 。

       ∴A（2， ），B（6， ）。

       （2）直线l从y轴出发，沿x轴正方向运动与菱形OABC的两边相交有三种情况：

       ① 时，直线l与OA、OC两边相交（如图①）。

       ∵MN⊥OC，∴ON=t。

       ∴ 。

        。

       ②当 时，直线l与AB、OC两边相交（如图②）

        。

       ③当 时，直线l与AB、BC两边相交（如图③）

       设直线l与x轴交于点H。

       ∵

        ，

       ∴

        。

       ∴

        ，

       （3）由（2）知，当 时， ；

       当 时， ；

       当 时，配方得 ，

       ∴当t=3时，函数 。

       但t=3不在 内，

       ∴在 内，函数 的最大值不是 。

       而当t>3时，函数 随t的增大而减小，

       ∴当 。

       综上所述，当t=4秒时， 。

       四、三角形运动

       例4.（2006青岛）如图①，有两个形状完全相同的直角三角形ABC和EFG叠放在一起（点A与点E重合），已知AC=8cm，BC=6cm，∠C=90°，EG=4cm，∠EGF=90°，O是ΔEFG斜边上的中点。

       如图②，若整个ΔEFG从图①的位置出发，以1cm/s的速度沿射线AB方向平移，在ΔEFG平移的同时，点P从ΔEFG的顶点G出发，以1cm/s的速度在直角边GF上向点F运动，当点P到达点F时，点P停止运动，ΔEFG也随之停止平移。设运动时间为x(s)，FG的延长线交AC于H，四边形OAHP的面积为y（cm2）（不考虑点P与G、F重合的情况）。

       （1）当x为何值时，OP//AC？

       （2）求y与x之间的函数关系式，并确定自变量x的取值范围。

       （3）是否存在某一时刻，使四边形OAHP面积与ΔABC面积的比为13：24？若存在，求出x的值；若不存在，说明理由。

       （参考数据：

        ）

       解：（1）∵RtΔEFG∽RtΔABC，

       ∴ 。

       ∴ 。

       ∵当P为FG的中点时，OP//EG，EG//AC，

       ∴OP//AC。

       ∴ 。

       ∴当x为1.5s时，OP//AC。

       （2）在RtΔEFG中，由勾股定理得：EF=5cm。

       ∵EG//AH，

       ∴ΔEFG∽ΔAFH。

       ∴ 。

       ∴ 。

       ∴ 。

       过点O作OD⊥FP，垂足为D。

       ∵点O为EF中点，

       ∴ 。

       ∵ ，

       ∴

       （3）假设存在某一时刻x，使得四边形OAHP面积与ΔABC面积的比为13：24。

       则

       ∵0<x<3，

       ∴当 时，四边形OAHP面积与ΔABC面积的比为13：24。

       五、矩形运动

       例5.（2006南安）如图所示，在直角坐标系中，矩形ABCD的边AD在x轴上，点A在原点，AB=3，AD=5。若矩形以每秒2个单位长度沿x轴正方向作匀速运动。同时点P从A点出发以每秒1个单位长度沿A—B—C—D的路线作匀速运动。当P点运动到D点时停止运动，矩形ABCD也随之停止运动。

       （1）求P点从A点运动到D点所需的时间；

       （2）设P点运动时间为t（秒）。

       ①当t=5时，求出点P的坐标；

       ②若ΔOAP的面积为s，试求出s与t之间的函数关系式（并写出相应的自变量t的取值范围）。

       解：（1）P点从A点运动到D点所需的时间= （秒）

       （2）①当t=5时，P点从A点运动到BC上，

       此时OA=10，AB＋BP=5，

       ∴BP=2

       过点P作PE⊥AD于点E，

       则PE=AB=3，AE=BP=3

       ∴

       ∴点P的坐标为（12，3）。

       ②分三种情况：

       （i）当 时，点P在AB上运动，

       此时OA=2t，AP=t

       （ii）当 时，点P在AB上运动，此时OA=2t

       ∴

       （iii）当8<t<11时，点P在CD上运动，

       此时OA=2t，

       ∴

       综上所述，s与t之间的函数关系式是：当 时， ；当 时，s=3t；当8<t<11时，

       六、圆的运动

       例6.（2006南昌）已知抛物线 ，经过点A（0，5）和点B（3，2）

       （1）求抛物线的解析式；

       （2）现有一半径为1，圆心P在抛物线上运动的动圆，问⊙P在运动过程中，是否存在⊙P与坐标轴相切的情况？若存在，请求出圆心P的坐标；若不存在，请说明理由；

       （3）若⊙Q的半径为r，点Q在抛物线上、⊙Q与两坐轴都相切时求半径r的值。

       解：（1）由题意，得

       解得

       抛物线的解析式为

       （2）当⊙P在运动过程中，存在⊙P与坐标轴相切的情况。（如图1）

       图1

       设点P坐标为（ ， ）

       则当⊙P与y轴相切时，有

       由

       ∴P1（－1，10），

       由 ，得

       ∴P2（1，2）

       当⊙P与x轴相切时有

       ∵抛物线开口向上，且顶点在x轴的上方。

       ∴y0=1

       由 ，得 ，解得 ，B（2，1）

       综上所述，符合要求的圆心P有三个，其坐标分别为：

       P1（－1，10），P2（1，2），P3（2，1）

       （3）设点Q坐标为（x，y），则当⊙Q与两条坐标轴都相切时（如图2），有 由y=x得 ，

       即 ，解得 ；

       由 ，得 。

       即 ，此方程无解

       ∴⊙O的半径为

中考数学试题参考(附解析)

       2009年数学中考模拟试题七

       考生须知：

       1、 考试卷分试题卷和答题卷两部分。满分120分，考试时间为120分钟。

       2、 答题前，必须在答题卷上填写班级、姓名、学号、试场号和座位号。

       3、 所有答案都必须做在答题卷标定的位置上，务必注意试题序号和答题序号相对应。

       4、 考试结束后，只需上交答题卷。

       请用铅笔将答案卷上的准考证号和学科名称所对应的括号或方框内涂黑，然后开始答题

       一、仔细选一选 (本题有10个小题, 每小题3分, 共30分)

       1、 -3的绝对值是（ ）

        A．-3 B．3 C．-1/3 D．1/3

       2、某市2007年的最高气温是39℃，最低气温是零下7℃，则计算该市2007年的温差，下列各式正确的是( )

        A.（＋39）－（－7） B. （＋39）＋（－7）

        C. （＋39）＋（＋7） D. （＋39）－（＋7）

       3、 在直角坐标系中，点M（1，2）关于y轴对称的点的坐标为（ ）

        A．（1，-2） B．（2，-1） C．（-1，-2） D．（-1，2）

       4、右图中几何体的主视图是（ ）

       5、2007年，中国月球探测工程的“嫦娥一号”卫星发射升空飞向月球，已知地球距离月球表面约为384000千米，那么这个距离用科学记熟法且保留三个有效数字表示为（ ）

       A．3.840×104千米 B．3.84×104千米 C．3.84 ×105千米 D．3.84×106千米

       6、已知等腰三角形的一个内角是30°，那么这个等腰三角形顶角的度数是（ ）

        A . 75° B . 120° C .30° D . 30°或120°

       7、在平面直角坐标系中，把直线y=2x向右平移一个单位长度后，其直线解析式为（ ）

        A. y=2x+1 B. y=2x-1 C. y=2x+2 D. y=2x-2

       8、把 x2-4分解因式的结果是（ ）

       A.(x-2) 2 B. (X+4)(X-4) C . (x-4)2 D (x+2)(x-2)

       9、如图，在⊙O中，弦AB，CD相交于点E。已知∠ECB＝60°，

       ∠AED＝65°，那么∠ADE的度数是（ ）

        A. 40° B. 15° C. 55° D. 65°

       10、我国股市交易中，每买卖一次需缴千分之七点五的各种费用。某投资者以每股10元的价格买入上海某股票1000股，当该股票涨到12元时全部卖出，该投资者实际赢利为（ ）

        A．2000元 B. 1925元 C . 1835元 D . 1910元

       二. 认真填一填 (本题有6个小题, 每小题4分, 共24分)

       11、抛物线 +3与坐标轴的交点共有 个。

       12、P为线段AB=8cm的黄金分割点，则AP= cm。

       13、不等式组 的整数解为

       14、已知关于x的一元二次方程m2x2+(2m-1)x+1=0有两个不相等的实数根，则m的取值范围是

       15、从1到10这十个自然数中，任意取出两个数，它们的积大于10的概率是 。

       16、如右图，直角三角形ABC中，∠C=90°，∠A=30°，点0在斜边AB上，半径为2的⊙O过点B，切AC边于点D，交BC边于点E，则由线段CD，CE及弧DE围成的隐影部分的面积为

       三. 全面答一答 (本题有8个小题, 共66分)

       17．（本题6分）求下列各式的值：

       （1） ＋ （2）已知 ，求 的值.

       18、（本小题6分）以O点为位似中心，在按位似比为2：1将图形缩小，请在O的另一侧画出它的位似图形。

       19、（本题6分）桌面上有15张扑克牌，甲、乙两人轮流取，每次最少取一张，最多取三张，谁取走最后一张谁就赢。

       （1）这个游戏规则对于甲、乙两方公平吗？

       （2）是先取者毕胜，还是后取者毕胜？有何致胜秘诀？

       （3）若将上面的15张扑克换成n张（n是不小于4的正整数），情况有如何？

       20、（本题8分）在平面上有且只有四个点，这四个点有一个独特的性质：每两点之间的距离有且只有两种长度，例如正方形ABCD四个顶点A，B，C，D，有AB=BC=CD=DA,AC=BD，请画出具有这种独特性质的另外四种不同的图形，并标明相等的线段

       21、（本题8分）如图，某电信公司计划修建一条连接B、C两地的电缆。测量人员在山脚A点测得B、C两地的仰角分别为30°、45°，在B处测得C地的仰角为60°，已知C地比A地高200m，求电缆BC的长（结果保留根号）.

       22、（10分）某体育用品商场为推销某一品牌运动服，先做了市场调查，得到数据如下表：

       卖出价格x(元／件) 50 51 52 53

        销售量p(件) 500 490 480 470

       (1)以x作为点的横坐标，p作为纵坐标，把上表中的数据，在图中的直角坐标系中描出相应的点，观察连结各点所得的图形，判断p与x的函数关系，并求出p与x的函数关系式；

       (2)如果这种运动服的买入价为每件40元，试求销售利润y(元)与卖出价格x(元／件)的函数关系式(销售利润=销售收入-买入支出)；

       (3)在(2)的条件下，当卖出价格为多少时，能获得最大利润?

       23、（本题10分）如图，从一个半径为1的圆形铁皮中剪下一个圆心角为 的扇形BAC．

       （1）求这个扇形的面积；

       （2）若将扇形BAC围成一个圆锥的侧面，这个圆锥的底面直径是多少？

       能否从最大的余料③中剪出一个圆做该圆锥的底面？请说明理由．

       24．（本题12分） 设抛物线 与x轴交于两个不同的点A（－1，0）、B（m，0），与y轴交于点C.且∠ACB＝90°.

       （1）求m的值；

       （2）求抛物线的解析式，并验证点D（1，－3 ）是否在抛物线上；

       （3）已知过点A的直线 交抛物线于另一点E. 问：在x轴上是否存在点P，使以点P、B、D为顶点的三角形与△AEB相似？若存在，请求出所有符合要求的点P的坐标. 若不存在，请说明理由.

       2009年数学中考模拟试题七

       答题卷

       一、选择题

       题号 1 2 3 4 5 6 7 8 9 10

       答案

       二、填空题：

       11．____________12．____________13．_________________14．______________

       15．______________16．_________________

       三. 全面答一答 (本题有8个小题, 共66分)

       17．（本小题6分）

       （1） ＋

       （2）已知 ，求 的值.

       18．（本小题6分）

       19．（本小题6分）

       20．（本小题8分）

       21．（本小题8分）

       22．（本小题10分）

       （1）

       （2）

       （3）

       23．（本小题10分）

       24．（本小题12分）

       2009年数学中考模拟试题七

       参考答案

       一、选择题

       题号 1 2 3 4 5 6 7 8 9 10

       答案 B A D A C D D D C C

       二、填空题：

       11．__三__ 12． 13．_-2_、-1、0、1__

       14． 15． 16．

       三. 全面答一答 (本题有8个小题, 共66分)

       17、（1） ＋

        ＝1－ ＋（ －1） （2分）

        =0 （1分）

       （2）已知 ，求 的值.

        解：∵ ∴x= y （1分）

        ∴ = = = （2分）

       18、（本小题6分）写出已知、求证得2分，结论1分，图形3分（图略）

       19．（本小题6分）（1）不公平（2分）

       （2）是先取者赢， （1分）

       因为为了要取得最后一根，甲必须最后留下零根火柴给乙，故在最后一步之前的轮取中，甲不能留下1根或2根或3根，否则乙就可以全部取走而获胜。如果留下4根，则乙不能全取，则不管乙取几根（1或2或3），甲必能取得所有剩下的火柴而赢了游戏。同理，若桌上留有8根火柴让乙去取，则无论乙如何取，甲都可使这一次轮取后留下4根火柴，最后也一定是甲获胜。由上分析可知，甲只要使得桌面上的火柴数为4、8、12、16...等让乙去取，则甲必稳操胜券。因此若原先桌面上的火柴数为15，则甲应取3根。（∵15-3=12） （2分）

       (3)还是先取者赢 （1分）

       20．（本小题8分）存在这些图形:1、一顶角为60度的菱形；2、正方形 ；3、一个正三角形+顶角150度的等腰三角形构成的四边行(等腰三角形的底为正三角形的边) ；4、一个等腰三角形+内部一点，使得该点到3个顶点的距离均等于底边；5、一内角为72度且上底等于腰的等腰梯形 ；6、正三角形+心（每答出一种得2分，答全四种得8分）

       21．（本小题8分）画BE、CF均垂直于AM，垂足分别为E、F；画BD⊥CF于D.

       则四边形BEFD是矩形. 设BD=x，由题意得

       AF=CF=200，EF=BD=x,AE=200- x （2分）

       ∵∠CBD=60°，∴CD=tan60°?BD= x，BE=DF=200－ x……（2分）

       ∵ = tan∠BAE= tan30°= ，

       即 = ,……（2分）

       解得x = ，

       ∴BC=2x= （m）……（2分）

       22．（本小题10分）

       （1）图略 （2分）

        p是x的一次函数 （1分），

        p=-10x+1000 （2分）；

       （2）y=px-40p=(-10x+1000)(x-40)=-10x2+1400x-40000 （2分）

       (3) y=-10(x-70)2+9000 （2分） 当x=70元时，y最大=9000元 （1分）

       23．（本小题10分）

       （1）∵∠A为直角，BC＝2，∴扇形半径为 （2分） ∴S扇＝ （2分）

        （2）设围成圆锥的底面半径为r，则2πr= （2分）

       延长AO分别交弧BC和⊙O于E、F，而EF＝2 ＜ （2分）

       ∴不能从最大的余料③中剪出一个圆做该圆锥的底面. （2分）

       24．（本小题12分）

       解：（1）令x＝0，得y＝－2 ∴C（0，－2）……（1分）

       ∵∠ACB＝90°，CO⊥AB ，∴△AOC ∽△COB ，∴OA?OB＝OC2

       ∴OB＝ ∴m＝4 （2分）

       （2）将A（－1，0），B（4，0）代入 ，解得

       ∴抛物线的解析式为 ……（2分）

       当x=1时， =－3，∴点D（1，－3）在抛物线上。……（1分）

       （3）由 得 ，∴E（6，7）……（2分）

       过E作EH⊥x轴于H，则H（6，0），

       ∴ AH＝EH＝7 ∴∠EAH＝45°

       作DF⊥x轴于F，则F（1，0）

       ∴BF＝DF＝3 ∴∠DBF＝45°

       ∴∠EAH=∠DBF=45°

       ∴∠DBH=135°，90°<∠EBA<135°

       则点P只能在点B的左侧，有以下两种情况：

       ①若△DBP1∽△EAB，则 ,∴

       ∴ ，∴ ……（2分）

       ②若△ ∽△BAE，则 ,∴

       ∴ ∴ ……（2分）

       综合①、②，得点P的坐标为：

重庆一中初2011级初三(下)6月中考数学模拟试题的第25题（今明两天内）

       中考数学试题参考(附解析)

       　一、选择题(本题有10小题，每小题3分，共30分，请选出各题中一个符合题的正确选项)

       　1. 下列各组数中，互为相反数是( ▲ )

       　A.3和 B.3和-3 C.3和- D.-3和-

       　2. 如图，直线AB∥CD，A=70，C=40，则E等于( )

       　A.30 B. 40 C. 60 D. 70

       　3. 某市五月份连续五天的日最高气温分别为23、20、20、21、26(单位：C)，这组数据

       　的中位数和众数分别是( )

       　A. 22C，26 B. 22C，20 C. 21C，26 D. 21C，20C

       　4.不等式组 的解集是( )

       　A. B. C. D.

       　5.在水平的讲台上放置圆柱形水杯和长方体形粉笔盒(右图)，则它的主视图是( )

       　A.图① B.图② C.图③ D.图④

       　6. 若反比例函数 的图象经过点 ，则这个函数的图象一定经过点( )

       　A. B. C. D.

       　7. 一个圆形人工湖如图所示，弦AB是湖上的一座桥.已知桥AB长100m，测得ACB=45.则

       　这个人工湖的直径AD为 ( )

       　A. B.

       　C. D.

       　8.一把大遮阳伞，伞面撑开时可近似地看成是圆锥形，

       　如图，它的母线长是2. 5米，底面半径为2米，则做这

       　把遮阳伞需用布料的面积是( )平方米(接缝不计)

       　A. B. C. D.

       　9. 如图是有关x的代数式的方阵，若第10行第2项的值为1034，

       　则此时x的值为( )

       　A. 10 B. 1 C. 5 D. 2

       　10. 已知△ABC中,D,E分别是AC,AB边上的中点，BDCE与

       　点F，CE=2,BD=4，则△ABC的面积为( )

       　A. B.8 C.4 D.6

       　卷Ⅱ

二、填空题(本题有6小题，每题4分，共24分)

       　11.函数 中自变量x的取值范围是 .

       　12.分解因式： .

       　13.如图，在ABC中，M、N分别是AB、AC的中点，

       　且A +B=136，则ANM=

       　14.除颜色外完全相同的五个球上分别标有1，2，3，4，5五个数字，

       　装入一个不透明的口袋内搅匀.从口袋内任摸一球记下数字后放

       　回.搅匀后再从中任摸一球，则摸到的两个球上数字和为5的概

       　率是

       　15.(2012扬州)如图，将矩形ABCD沿CE折叠，点B恰好落在

       　边AD的F处.若 ，则tanDCF的值是_________.

       　16.(原创题)已知平面直角坐标系中，O为坐标原点，

       　点A坐标为(0，8)，点B坐标为(4，0)，点E是直

       　线y=x+4上的一个动点，若EAB=ABO，则点

       　E的坐标为 。

三、解答题(本题有8小题，共66分，各小题都必须写出解题过程).

       　17.(本题6分)计算： sin45-|-3|+

       　18.(本题6分)解方程： .

       　19.(本题6分)已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A(-2，0)，与反比例函数在第一象限内的图象交于点B(2，n)，连结BO，若 .

       　(1)求该反比例函数的解析式;

       　(2)若直线AB与y轴的交点为C，求△OCB的面积.

       　20.(本题8分)如图，AB是⊙O的直径，CD是⊙O的切线，切点为C，BECD，垂足

       　为E，连接AC、BC.

       　(1)求证：BC平分

       　(2)若ABC=30，OA=4，求CE的长.

       　21.(本题8分)浙江省委十三届四次全会提出，要以治污水、防洪水、排涝水、保供水、抓节水五水共治的重大决策,某中学为了提高学生参与五水共治的积极性举行了五水共治知识竞赛，所有参赛学生分别设有一、二、三等奖和纪念奖，获奖情况已汇制成如图所示的两幅不完整的统计图，根据图中所经信息解答下列问题：

       　(1)这次知识竞赛共有多少名学生?

       　(2)浙江省委十三届四次全会提出，要以治污水、防洪水、排涝水、保供水、抓节水五水共治的重大决策, 二等奖对应的扇形圆心角度数，并将条形统计图补充完整;

       　(3)小华参加了此次的知识竞赛，请你帮他求出获得一等奖或二等奖的概率。

       　22.华宇公司获得授权生产某种奥运纪念品，经市场调查分析，该纪念品的销售量 (万件)与纪念品的价格 (元/件)之间的函数图象如图所示，该公司纪念品的生产数量 (万件)与纪念品的价格 (元/件)近似满足函数关系式 ，若每件纪念品的价格不小于20元，且不大于40元.

       　请解答下列问题：

       　(1)求 与 的函数关系式，并写出 的取值范围;

       　(2)当价格 为何值时，使得纪念品产销平衡(生产量与销售量相等);

       　(3)当生产量低于销售量时，政府常通过向公司补贴纪念品的价格差来提高生产量，促成新的产销平衡.若要使新的产销平衡时销售量达到46万件，政府应对该纪念品每件补贴多少元?

       　23.(10分)小华用两块不全等的等腰直角三角形的三角板摆放图形.

       　(1)如图①所示两个等腰直角△ABC，△DBE，两直角边交于点F，连接BF、AD，求证：BF=AD;

       　(2)如果小华将两块三角板△ABC，△DBE如图②所示摆放，使D、B、C三点在一条直线上，AC、DE的延长线相交于点F，过点F作FG∥BC，交直线AE于点G，连接AD，FB，求证：FG=AC+DC;

       　(3)在(2)的条件下，若AG= ，DC=5，将一个45角的顶点与点B重合，并绕点B旋转，这个角的两边分别交线段FG于P、Q两点(如图③)，若PG=2，求线段FQ的长.

       　24.(本题12分)已知：如图，抛物线y=ax2+bx+c与x轴交于点A(0，4)、E(0，-2)两点，与y轴交于点B(2，0)，连结AB。过点A作直线AKAB，动点P从点A出发以每秒 个单位长度的速度沿射线AK运动，设运动时间为t秒，过点P作PCx轴，垂足为C，把△ACP沿AP对折，使点C落在点D处。

       　(1)求抛物线的解析式;

       　(2)当点D在△ABP的.内部时，△ABP与△ADP不重叠部分的面积为S，求S与t之间的函数关系式，并直接写出t的取值范围;

       　(3)是否存在这样的时刻，使动点D到点O的距离最小，若存在请求出这个最小距离，若不存在说明理由.

       　数学模拟试卷

参考答案

       　一、选择题(本题有10小题，每小题3分，共30分)

       　1-5:BADCB 6-10:DBCDA

       　二、填空题(本题有6小题，每题4分，共24分)

       　11:

       　12：

       　13：44

       　14：

       　15：

       　16：

       　三、解答题(本题有8小题，共66分，各小题都必须写出解题过程).

       　17.

       　18. 经检验 是原方程的解

       　19.(1) 3分 (2) 6分

       　20.(本题8分)证明：连接OC

       　∵CD切⊙O于C

       　OCCD

       　∵BECD

       　OC∥BE

       　OCB=EBC

       　∵OC=OB

       　OCB=OBC

       　EBC=OBC

       　BC平分ABE4分

       　(2) 过A做CFAB于F

       　∵AB是⊙O的直径

       　ACB=90

       　∵ABC=30A=60

       　在Rt△ACF中，A=60，

       　∵BC平分ABE，CFAB，∵CEBE

       　8分(也可用相似求解)

       　21. 解：(1)200名2分

       　(2)72，二等奖人数为40名5分

       　(3) 8分

       　22、解：(1)设 与 的函数解析式为： ，将点 、 代入 得：

       　解得： 2分

       　与 的函数关系式为： 3分

       　(2)当 时，有 解得： 4分 当 时，有 解得：

       　当价格为30元或38元，可使公司产销平衡5分

       　(3)当 时，则 ， 6分

       　当 时，则 ， 7分

       　政府对每件纪念品应补贴1元. 8分

       　23. 解：(1)证明：∵△ABC，△DBE是等腰直角三角形，

       　△CDF也是等腰直角三角形;

       　CD=CF，(1分)

       　又∵BCF=ACD=90，AC=BC

       　△BCF≌△ACD，(2分)

       　BF=AD;(3分)

       　(2)证明：

       　∵△ABC、△BDE是等腰直角三角形

       　ABC=BAC=BDE=45，

       　∵FG∥CD，

       　G=45，

       　AF=FG;(4分)

       　∵CDCF，CDF=45，

       　CD=CF，(5分)

       　∵AF= AC +CF，

       　AF=AC+DC.

       　FG=AC+DC.(6分)

       　(3)过点B作BHFG垂足为H，过点P作PKAG于点K，(7分)

       　∵FG∥BC，C、D、B在一条直线上，

       　可证△AFG、△DCF是等腰直角三角形，

       　∵AG= ，CD=5，

       　根据勾股定理得：AF=FG=7，FD= ，

       　AC=BC=2，

       　BD=3;

       　∵BHFG，

       　BH∥CF，BHF=90，

       　∵FG∥BC，

       　四边形CFHB是矩形， (8分)

       　BH=5，FH=2;

       　∵FG∥BC，

       　G=45，

       　HG=BH=5，BG= ;

       　∵PKAG，PG=2，

       　PK=KG= ，

       　BK= ﹣ =4 ;(9分)

       　∵PBQ=45，HGB=45，

       　GBH=45，

       　2;

       　∵PKAG，BHFG，

       　BHQ=BKP=90，

       　△BQH∽△BPK，

       　，

       　QH= ，(9分)

       　(10分)

       　24、(12分)

       　(1)解：

       　抛物线的解析式为y= x2+ x+24分

       　(2)由AP= t和AOB∽PCA 可求得AC=t，

       　PC=2t5分

       　S=SABP-SADP= 2 t- 2tt

       　=-t2+5t6分

       　t的取值范围是0

       　(3)连结CD，交AP于点G，过点作D Hx轴，垂足为H

       　易证△ACG∽△DCH∽△BAO且OB：OA：AB=1：2：

       　因为DAP=CAP，点D始终在过点A的一条定直

       　线上运动，设这条定直线与y轴交于点E

       　当AC=t=1时，DC=2CG=2 =

       　DH= ，HC=

       　OH=5- =

       　点D的坐标为( ， )10分

       　可求出直线AD的解析式为y=- x+ ，点E的坐标为(0， )

       　可求得AE= 11分

       　此时点RT△EAO斜边上的高即为OD的最小距离，为 = 12分

       25.解：(1)猜想：y与x是一次函数关系.设y=kx+b(k≠0)

则?解得：?

∴y=4x+600?…………?2分

验证：当x=200时，y=4×200+600=1400

结论：猜想成立，即y=4x+600?…………?3分

(2)?w=y﹒p=(4x+600)﹒(-5x+9000)

由(4x+600)(-5x+9000)=0得x1=?-150,x2?=1800

∴对称轴：?

       ∵开口向下，对称轴是x=825，而x是100的倍数

∴当x=800时，?=（4×800+600）（-5×800+9000）=19000000

       ∴当政府每亩补贴800元时，该地苗圃收益最大，最大值为19000000元.?……?7分

(3)当x=800时，y=4x+600=4×800+600=3800（亩）

       P=-5x+9000=-5×800+9000=5000(元)

       由题意得：3800（30-a）%×[5000(1+3a%)-1000]=3990000…………?9分

       整理得：3a2-10a-300=0

       △ =(-10)2-4×3×(-300)=3700

       ∴?

       ∴a≈11.8=12?(舍去)

答：a的值约为1?2.?……

       非常高兴能与大家分享这些有关“初三数学中考模拟试题”的信息。在今天的讨论中，我希望能帮助大家更全面地了解这个主题。感谢大家的参与和聆听，希望这些信息能对大家有所帮助。